Prospect Theory Definition
Prospect theory is a psychological account that describes how people make decisions under conditions of uncertainty. These may involve decisions about nearly anything where the outcome of the decision is somewhat risky or uncertain, from deciding whether to buy a lottery ticket, to marry one’s current romantic partner, to undergo chemotherapy treatment, or to invest in life insurance.
Prospect theory predicts that people go through two distinct stages when deciding between risky options like these. In the first phase, decision makers are predicted to edit a complicated decision into a simpler decision, usually specified as gains versus losses. Purchasing a car is simplified into losing $20,000 and gaining a car, whereas buying a lottery ticket is simplified into losing $1 and gaining a small chance to win $100,000. A key feature of this editing phase is that the way in which people edit or simplify a decision may vary from one moment to the next, depending on situational circumstances. A person may think of a lottery as a .001% chance to gain $1 million, for instance, or as a 99.999% chance to lose $1. People make decisions based on these edited prospects, and the way that prospects are edited is therefore a critical determinant of the decisions they will make.
In the second phase, decision makers choose between the edited options available to them. This choice is based on two dimensions: the apparent value of each attribute or option and the weight (similar, although not identical to, the objective likelihood) assigned to those values or options. These two features—overall value and its weight—are then combined by the decision maker, and the option with the highest combined value is chosen by the decision maker.
The most interesting feature of prospect theory for most psychologists is that it predicts when (and why) people will make decisions that differ from perfectly rational or normative decisions, and has therefore figured prominently in explanations of why people make a variety of transparently bad decisions in daily life.
Prospect Theory Background and History
Decision-making research before the 1970s was dominated by normative theories that prescribe how people “ought” to make decisions in a perfectly rational way, and many implicitly assumed that most people, in daily lives, followed these normative rules. Prospect theory was a notable departure from these existing theories because it offered a descriptive theory of how people actually make decisions, rather than providing a perfectly rational account of how they ought to do so.
The simplest way to choose between risky options is to choose the option with the highest expected value—the likelihood that an option will occur, multiplied by the value of that option. Imagine, for instance, that you are deciding whether to pay $1 for a lottery ticket that offers a 10% chance of winning $10. The expected value of this lottery ticket is $1 (0.1 x $10), the same as the cost of the ticket. Rationally speaking, you should therefore be perfectly indifferent about buying this ticket or not. The problem, noted by both economists and psychologists, is that rational theories did not always describe people’s actual behavior very well. Few people, for instance, would actually purchase the lottery ticket in the last example. The certain loss of $1 simply does not compensate for the 10% chance of winning $10 and a 90% chance of winning nothing. In general, research found that people were more averse to taking risks than the expected value of outcomes would predict.
The inability of expected value calculations to explain people’s decisions then led to the development of expected utility theory, which essentially incorporated people’s attitude toward risk into their expected value calculations. Expected utility theory assumed that attitudes toward risk were stable within individuals, were not influenced by the way a particular decision was described (or framed), and was not influenced by the mood or situational context of the decision maker. However, experiments again revealed that decision makers often violate the predictions made by expected utility theory. For instance, a terminal cancer treatment with a 1 in 10 chance of saving the patient’s life is identical to a cancer treatment with a 9 in 10 chance of death (assuming people can only live or die), and yet terminally ill cancer patients themselves would likely be more interested in pursuing this treatment when described as the likelihood of living than when described as the likelihood of dying.
Prospect theory was motivated by these failures of rational models to describe actual decision making in everyday life. Daniel Kahneman, one of the founders of prospect theory along with the late Amos Tversky, won the 2002 Nobel Prize in economics, at least in part, for this work.
Value and Weighting Functions
Prospect theory’s central prediction is that choices between uncertain outcomes are determined by the combination of an outcome’s apparent value (predicted by the value function) and the importance or weight assigned to a particular outcome (called the weighting function).
Value Function
There are three critical aspects of the value function. First, value is assigned to changes in value rather than to absolute value. Almost no attribute can be judged in isolation, but can be judged only in relation to something else. A person is tall, for instance, only in comparison with others who are shorter. Or a person is happy only in relation to those who are sadder. So too, prospect theory predicts that the value assigned to an option is determined only by comparison with other options, and the option used in this comparison is therefore of critical importance. Winning an all-expenses-paid trip to Florida might sound wonderful compared with an all-expenses-paid trip across the street. But that trip to Florida might not sound nearly as wonderful when compared with an all-expenses-paid trip to Fiji. This comparison in prospect theory is called a reference point, and the value of an object is determined by the change in value between an object under consideration and that reference point, rather than by the absolute value of an object. This means that people might accept an option in one situation that they reject in another.
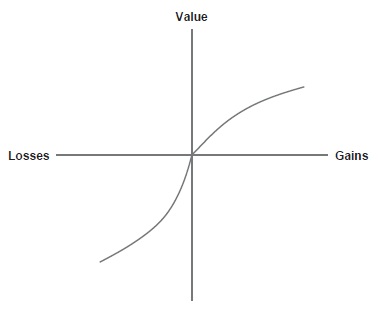
Figure 1. A Hypothetical Value Function
Second, the value function is S-shaped , and predicted to be concave for gains above the reference point and convex for losses below the reference point. This means that differences between small gains or losses close to the reference point are assigned a high value, whereas differences farther away from the reference point are assigned smaller values. The difference between winning $5 versus $10 seems rather large, for instance, but winning $1,000 and winning $1,005 seems relatively small, even though the objective difference ($5) is identical.
Third, the value function is steeper for losses than for gains. This means that a loss is assigned greater value than is a gain of an objectively identical amount. The prospect of losing $10 in a gamble, for instance, seems worse than the prospect of gaining $10 seems good. This difference helps explain why few people are interested in betting money on the outcome of a fair coin, even though the probability of winning money on this gamble is identical to the probability of losing money.
These two features of the value function have at least three profound effects on decision making. First, the S-shape of the value function means that minor changes near a reference point are likely to have a much more dramatic influence on decisions than are equivalent changes further from the reference point.
A person might drive across town, for instance, to buy a $10 book on sale for $5, but would not do so to buy a $1,005 TV on sale for $1,000. Or a person might be very enthusiastic about taking a new drug that reduces his or her risk of contracting a disease from 5% to 1%, but much less enthusiastic about a new drug that reduces the risk from 50% to 46%. Second, the asymmetry between gains and losses means that people will generally be loss-averse, which explains why people are not indifferent to gambles that have an equal probability of losing versus winning the same amount of money. What is more, this asymmetry explains why framing a decision in terms of gains or losses can have such a profound influence on behavior. People are unlikely to choose an option framed as a loss from a reference point compared with the same option framed as a gain from a reference point. Third, the asymmetry between gains and losses means that people are likely to be risk seeking in the domain of losses, but risk averse in the domain of gains. Because the prospect of losses hurts more than the prospect of gains feels good, people are likely to take greater risks to avoid a foreseeable loss than to ensure a foreseeable gain. People who fear falling short of a goal, for instance, may choose to adopt a riskier course of action to eventually achieve that goal (that may leave them even further from their goal), compared with people who believe they will exceed their goal.
Weighting Function
Rational models of decision making assume that people multiply the perceived value of an outcome by the objective likelihood that the outcome will occur. Prospect theory modifies this slightly and predicts that instead, people multiply the perceived value of an outcome by a decision weight. The major difference between the decision weights and objective probabilities is observed with extreme probabilities (either very low, e.g., 1%, or very high, e.g., 99%). For instance, moving from having no chance of contracting a terminal illness to having a 1% chance has a much larger effect on one’s decision making than moving from a 50% chance to a 51% chance. Although the increase in the likelihood of contracting a terminal illness is the same (1%), the influence this increase has on one’s decision—considered its weight in the decision— is not. In general, people tend to overweight low-probability events in judgment, which helps explain the irrational appeal of gambling and insurance for very low-probability events. At the other extreme, people tend to underweight highly certain outcomes. People will pay much less, for instance, for a lottery in which they have a 99% chance of winning $1,000 than they will for a lottery in which they have a 100% chance of winning $1,000, but there is little difference between the amount people would pay for a 50% versus 51% chance of winning $1,000. Again, the objective difference in probabilities (1%) is identical, but its impact on one’s decision is not.
Prospect Theory Evidence
Support for prospect theory can be found in a wide variety of disciplines, including sociology, psychology, and many areas within economics. Much of the empirical support comes from studies in which people make hypothetical or real choices between gambles. These gamble studies are ideal because they allow researchers to clearly specify the value and probabilities associated with each gamble, and provide an analogy to many, if not all, risky decisions made in daily life. Substantial empirical support exists for the major tenets of prospect theory: the importance of reference points in decision making, the asymmetry between gains and losses of equivalent magnitudes, and the weighting function that overweights low-probability events and underweights high-probability events. Recent advances in prospect theory involved demonstrations in field settings (such as with New York taxi drivers), and the more complicated treatment of decisions with a very large number of possible outcomes (called cumulative prospect theory). None of these recent advances challenged the major tenets of the original formulation.
Prospect Theory Importance for Social Psychology
At its heart, social psychology investigates how situations—typically social situations—influence judgment and behavior. Prospect theory explains how situational variability in the way a decision is framed can have a dramatic impact on the decisions people make. These decisions are not restricted to any particular domain. They can be decisions to accept a financial gamble as much as they can be decisions about whether to marry one’s high-school sweetheart, whether to fund social welfare policies, or whether to help a person in need.
In particular, the overall prediction from prospect theory that judgments and decision are determined by comparisons to an existing reference point has figured prominently in many areas of social psychology. For instance, White Americans in public opinion surveys typically report that racial conditions have improved significantly more than Black Americans do. One of the reasons for this difference appears to be that minority groups frame their progress as falling short of a goal compared with majority groups and, therefore, are more likely to consider what still needs to be accomplished rather than what has already been gained. Research on social comparisons similarly highlights the importance of reference points for determining one’s self-concept, and research on social judgment shows that people often use their judgments as a reference point for others’ judgments.
The asymmetry between gains and losses has similarly influenced several areas of social psychology. For instance, people tend to react much more strongly to threatening social cues in the environment than to helpful or supportive social cues. This pattern has been termed the negativity bias and is both informed by, and an extension of, the gain-loss asymmetry documented by prospect theory. The gain-loss asymmetry has also figured prominently in theories of motivation and goal pursuit. Focusing on preventing a loss versus achieving a gain activates very different kinds of psychological states and behaviors, a line of research clearly inspired by the insights of prospect theory. Finally, people’s tendency to be risk seeking in the domains of losses but risk averse in the domain of gains has been applied to political attitudes for change versus stability and has therefore shed light on the origins of conservative versus liberal social attitudes.
One very specific phenomenon that has been of particular interest to social psychologists is the endowment effect. Empirical evidence demonstrates that people are more reluctant to give up or sell an item once they own it than they are interested in acquiring it if they do not. In the most common experimental demonstration, participants were randomly assigned to either receive a mug to take home or to receive no mug. Those who received a mug later state the amount of money they would ask to sell the item, and those who do not have a mug indicate the amount they would spend to buy the object. Despite being randomly assigned to own the mug, results show repeatedly that selling prices are higher than buying prices. The reason is that buyers are gaining an object and therefore value it less than do sellers who are losing an object. The power of this situational influence, unfortunately, is generally lost on buyers and sellers themselves who instead explain the other role’s behavior as an instance of greed—not wanting to pay or sell an object for what it is “really” worth.
References:
- Eibach, R. P., & Ehrlinger, J. (2006). Keep your eyes on the prize: Reference points and racial differences in assessing progress toward equality. Personality and Social Psychology Bulletin, 32, 66-77.
- Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263-291.
- Rottenstreich, Y., & Hsee, C. K. (2001). Money, kisses, and electric shocks: On the affective psychology of risk. Psychological Science, 12, 185-190.
- Thaler, R. H. (1980). Towards a positive theory of consumer choice. Journal of Economic Behavior and Organization, 1, 39-60.
- Tversky, A., & Kahneman, D. (2000). Advances in prospect theory: Cumulative representation of uncertainty. In D. Kahneman & A. Tversky (Eds.), Choices, values, and frames (pp. 44-65). New York: Cambridge University Press.
- Van Boven, L., Dunning D., & Loewenstein G. (2000). Egocentric empathy gaps between owners and buyers: Misperceptions of the endowment effect. Journal of Personality and Social Psychology, 79, 66-76.