Factor analysis is a statistical procedure for describing the interrelationships among a number of observed variables. Factor analysis is used to measure variables that cannot be measured directly, to summarize large amounts of data, and to develop and test theories. There are two broad categories of factor analysis: exploratory and confirmatory. Exploratory factor analysis techniques have a much longer history than confirmatory factor analysis techniques. Differences in the approaches lead to different uses (e.g., theory development versus theory confirmation).
Purposes
Factor analysis has three fundamental purposes. First, it is useful for measuring constructs that cannot readily be observed in nature. For example, we cannot hear, see, smell, taste, or touch intelligence, but it can be inferred from the assessment of observable variables such as performance on specific ability tests. Factor analysis is also helpful in the development of scales to measure attitudes or other such latent constructs by assessing responses to specific questions. Second, factor analysis is useful for summarizing a large amount of observations into a smaller number of factors. For example, there exist thousands of personality descriptors in the English language. Through factor analysis, researchers have been able to reduce the number of distinct factors needed to describe the structure of personality. Third, factor analysis is useful for providing evidence of construct validity (e.g., factorial, convergent, and discriminant validity). For example, if certain observable variables are theoretically related to one another, then factor analysis should demonstrate these theoretical relationships, simultaneously demonstrating that the same variables are reasonably uncorrelated with variables from other latent factors. All three of these uses of factor analysis can be employed in the development and testing of psychological theories.
Basic Factor Model
The basic factor analysis problem takes a number of observable variables and explains their interrelationships in a manner that is analogous to a regression equation. The common factor model is a regression equation in which the common factors act as predictors of the observed X variables. The basic factor model is depicted in Equation 1.
In this equation, X is the matrix of observed variables, L is the matrix of factor loadings or regression weights, f is the matrix of common factors, and u is the matrix of residuals. The goal is to explain the interrelationships among the X variables by the common factors, f, and the residual error terms, called uniqueness. The variance in X is partitioned into common and specific components. Unlike regression, however, the predictors, f, are unknown.
To provide a fictional example of this problem, suppose a number of supervisors are asked to rate the relevance of six personality characteristics to effective job performance by subordinates. The characteristics assessed are organized, systematic, careless, creative,
intellectual, and imaginative. Table 1 depicts the hypothetical correlation matrix for these variables. The factor analysis problem is to explain the relationships among these variables with fewer than six underlying latent factors. Organized, systematic, and careless are all correlated with one another, but they are not correlated with creative, intellectual, and imaginative. Likewise, creative, intellectual, and imaginative are all correlated with one another, but they are not correlated with organized, systematic, and careless. There are two sets of correlations reflecting two underlying factors.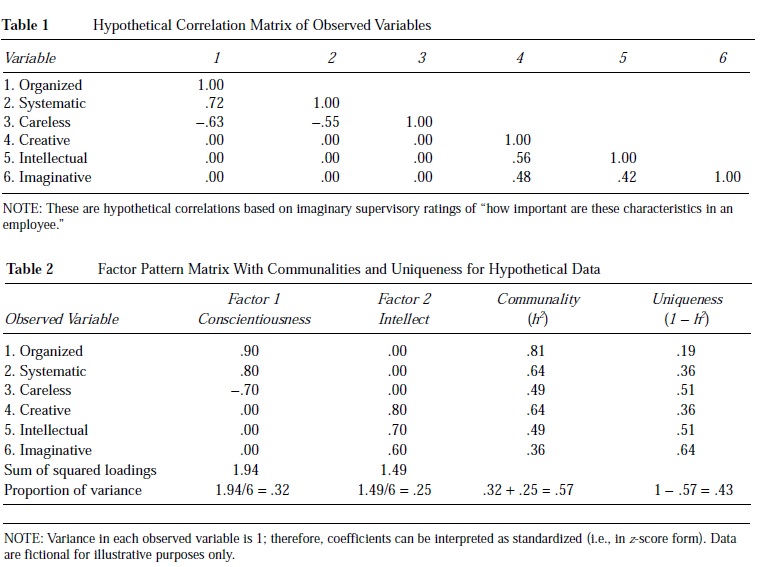
Table 2 depicts the factor pattern matrix for these variables and the corresponding latent factors. The pattern coefficients in Table 2 (columns 2 and 3) are the correlations of the observed variables with the factors. Different pattern or loading matrixes will present different types of correlations (e.g., Pearson correlations, partial correlations).
The communality (h2) in column 4 of Table 2 represents the variance that the variable has in common with the factors it represents. The communality is analogous to a squared multiple correlation in regression. The uniqueness in column 5 represents the variance specific to a variable and not accounted for by the factor. Uniqueness is analogous to the residual variance in the observed variable after accounting for the factors. The six fictitious variables represent two unobservable factors, each factor accounting for 36% to 81% of the variance in the observed variables.
In addition to the variance associated with the observed variables, the factor analysis solution describes the variance in the factors themselves. The sum of the squared loadings (SSL) for a set of variables describes each factor’s variance. Before any transformation in the factor loadings has taken place, these SSLs are called eigen values. Ideally, a small number of factors will account for a large amount of the variance in the observed variables. Table 2 shows that the factors account for 32% and 25%, for a total of 57% of the variance in the observed variables. The remaining 43% of the variance in the observed variables is not common to the factors.
Exploratory Factor Analysis
Typically, the goal of exploratory factor analysis (EFA) is to let the data determine the interrelationships among a set of variables. Although a researcher using EFA may have a theory relating the variables to one another, there are relatively few restrictions on the basic factor model in an EFA. This type of analysis has been useful in theory development and debate for more than a century.
Exploratory factor analysis is particularly appropriate in the early stages of theory development and in the early stages of scale or test development. First, EFA is useful in data reduction when interrelationships among variables are not specified beforehand. A researcher using EFA makes use of inductive reasoning by taking a number of observations and developing theory from those observations. In the example of high-performing employee characteristics, six personality variables were ultimately reduced to two factors. For subsequent analyses, then, only two variables need be discussed rather than the six original variables. Data reduction is particularly useful in alleviating the concerns of multi-collinearity (correlations that are too high) among a set of predictors. A second benefit of EFA is the ability to detect a general factor. When several specific cognitive ability tests are factor analyzed, one general factor tends to emerge, along with several specific factors. In the assessment of intelligence, for example, all ability tests correlate to some extent with the general factor of intelligence, or g.
Finally, EFA is particularly useful in scale or test development because it allows the researcher to determine the dimensionality of the test and detect cross-loadings (correlations of variables with more than one factor). Cross-loadings are generally not desirable. In scale development, it is advantageous to have items that relate to only one factor. For the previous example, the three variables representing conscientiousness do not cross-load onto intellect and vice versa.
Confirmatory Factor Analysis
The goal of confirmatory factor analysis (CFA) is to test theoretically derived hypotheses given a set of data. The basic factor model of Equation 1 is still relevant, but certain restrictions are imposed given the particular theoretical model being tested. For example, from the previous example, one could use CFA to impose restrictions on the factor pattern so that no cross-loadings are permitted. Developed during the 1960s, CFA is a newer statistical development than EFA (developed in 1904).
Confirmatory factor analysis is particularly useful in a deductive reasoning process. Specific hypothesis testing is possible when using CFA. For example, a researcher may address the statistical significance of individual factor loadings. In the previous example, given the relatively small correlation, one could determine with statistical certainty the degree to which the observed variable, imaginative, is correlated with the latent factor, intellect.
With CFA, it is possible to test the hypothesis that two factors versus only one factor (or any other numeric combination) underlie a set of data. In EFA, researchers rely on rules of thumb and intuition, which can lead the researcher astray, but in CFA, models can be explicitly compared through null hypothesis statistical testing. Another use of CFA is to assess the equivalence of parts of the basic factor model within a given data set. For example, one might hypothesize that all of the observed variables for intellect are equally related to intellect. With CFA, the equivalence of these relationships can be tested by imposing constraints on the loadings in the basic factor model (i.e., L in Equation 1).
It is also important to determine whether the results of a factor analysis are similar across demographic groups. Confirmatory factor analysis permits tests of invariance—that is, the equivalence of factor structure, loadings, uniqueness—across different groups (e.g., ethnic, gender, cultural) of individuals. A researcher may be interested in knowing whether the same hypothetical factor structure would emerge if responses from supervisors of manufacturing workers were compared with responses from supervisors of service workers. It may be the case that the observed variable do not relate to the latent factors in the same manner for the two groups. For example, the observed indicator systematic may be less related to the factor conscientiousness for service workers than for manufacturing workers. In a CFA that is testing for equivalence of factor loadings, a researcher can test the hypothesis that the correlations from the two groups are the same or different.
Confirmatory factor analysis has greater flexibility in control than EFA. With CFA, some factors may be specified as oblique (correlated with one another), whereas others are specified to be orthogonal (uncorrelated with one another). Within a single EFA, the factors are interpreted as either oblique or orthogonal but not a combination of the two. In addition, CFA allows the researcher to flexibly impose additional constraints subject to theory (e.g., allowing correlated uniqueness). However, a benefit of EFA is that no such theoretical constraints or specifications are needed. Therefore, if none exist, then EFA may be a better choice.
References:
- Gorsuch, R. L. (2003). Factor analysis. In J. A. Schinka & W. F. Velicer (Eds.), Handbook of psychology: Research methods in psychology (Vol. 2, pp. 143-164). Hoboken, NJ: Wiley.
- Hurley, A. E., Scandura, T. A., Schriesheim, C. A., Brannick, M. T., Seers, A., Vandenberg, R. J., & Williams, L. J. (1997). Exploratory and confirmatory factor analysis: Guidelines, issues, and alternatives. Journal of Organizational Behavior, 18, 667-683.
- Lance, C. E., & Vandenberg, R. J. (2002). Confirmatory factor analysis. In F. Drasgow & N. Schmitt (Eds.), Measuring and analyzing behavior in organizations: Advances in measurement and data analysis (pp. 221254). San Francisco: Jossey-Bass.
- Preacher, K. J., & MacCallum, R. C. (2003). Repairing Tom Swift’s electric factor analysis machine. Understanding Statistics, 2, 13-43.
- Thompson, B. (2004). Exploratory and confirmatory factor analysis: Understanding concepts and applications. Washington, DC: American Psychological Association.
- Vandenberg, R. J., & Lance, C. E. (2000). A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Organizational Research Methods, 3, 4-69.