The Analytic Hierarchy Process (AHP) is a powerful decision-making tool that has been widely adopted in various industries and fields of study. Developed by Thomas L. Saaty in the 1970s, AHP is a structured and systematic approach that helps individuals and organizations make complex decisions by breaking them down into smaller, more manageable parts. By using a hierarchical structure and mathematical calculations, AHP allows decision makers to evaluate and compare different criteria and alternatives, ultimately leading to the most rational and optimal decision. This method has proven to be highly effective in streamlining decision-making processes and has been applied in a wide range of fields, including business, engineering, healthcare, and public policy. In this article, we will explore the fundamentals of AHP and its practical applications, highlighting its importance in today’s fast-paced and competitive world.
A simple AHP hierarchy, with final priorities. The goal is to select the most suitable leader from a field of three candidates. The factors to be considered are Experience, Education, Charisma, and Age. According to the judgments of the decision makers, Dick is the strongest candidate, followed by Tom, then Harry. Their decision process is described in depth in an appendix to this article. The Analytic Hierarchy Process (AHP) is a structured technique for dealing with complex decisions. Rather than prescribing a “correct” decision, the AHP helps decision makers find one that best suits their goal and their understanding of the problem—it is a process of organizing decisions that people are already dealing with, but trying to do in their heads. Based on mathematics and psychology, the AHP was developed by Thomas L. Saaty in the 1970s and has been extensively studied and refined since then. It provides a comprehensive and rational framework for structuring a decision problem, for representing and quantifying its elements, for relating those elements to overall goals, and for evaluating alternative solutions. It has particular application in group decision making, and is used around the world in a wide variety of decision situations, in fields such as government, business, industry, healthcare, and education. Several firms supply computer software to assist in using the process. Users of the AHP first decompose their decision problem into a hierarchy of more easily comprehended sub-problems, each of which can be analyzed independently. The elements of the hierarchy can relate to any aspect of the decision problem—tangible or intangible, carefully measured or roughly estimated, well- or poorly-understood—anything at all that applies to the decision at hand. Once the hierarchy is built, the decision makers systematically evaluate its various elements by comparing them to one another two at a time, with respect to their impact on an element above them in the hierarchy. In making the comparisons, the decision makers can use concrete data about the elements, or they can use their judgments about the elements’ relative meaning and importance. It is the essence of the AHP that human judgments, and not just the underlying information, can be used in performing the evaluations. The AHP converts these evaluations to numerical values that can be processed and compared over the entire range of the problem. A numerical weight or priority is derived for each element of the hierarchy, allowing diverse and often incommensurable elements to be compared to one another in a rational and consistent way. This capability distinguishes the AHP from other decision making techniques. In the final step of the process, numerical priorities are calculated for each of the decision alternatives. These numbers represent the alternatives’ relative ability to achieve the decision goal, so they allow a straightforward consideration of the various courses of action. Uses and applications While it can be used by individuals working on straightforward decisions, the Analytic Hierarchy Process (AHP) is most useful where teams of people are working on complex problems, especially those with high stakes, involving human perceptions and judgments, whose resolutions have long-term repercussions. It has unique advantages when important elements of the decision are difficult to quantify or compare, or where communication among team members is impeded by their different specializations, terminologies, or perspectives. Decision situations to which the AHP can be applied include: The applications of AHP to complex decision situations have numbered in the thousands, and have produced extensive results in problems involving planning, resource allocation, priority setting, and selection among alternatives. Other areas have included forecasting, total quality management, business process re-engineering, quality function deployment, and the Balanced Scorecard. Many AHP applications are never reported to the world at large, because they take place at high levels of large organizations where security and privacy considerations prohibit their disclosure. But some uses of AHP are discussed in the literature. Recently these have included: AHP is sometimes used in designing highly specific procedures for particular situations, such as the rating of buildings by historic significance. It was recently applied to a project that uses video footage to assess the condition of highways in Virginia. Highway engineers first used it to determine the optimum scope of the project, then to justify its budget to lawmakers. Education and scholarly research Though using the Analytic Hierarchy Process requires no specialized academic training, it is considered an important subject in many institutions of higher learning, including schools of engineering and graduate schools of business. It is a particularly important subject in the quality field, and is taught in many specialized courses including Six Sigma, Lean Six Sigma, and QFD. The value of the AHP is recognized in developed and developing countries around the world. China is a good example — nearly a hundred Chinese universities offer courses in AHP, and many doctoral students choose AHP as the subject of their research and dissertations. Over 900 papers have been published on the subject in China, and there is at least one Chinese scholarly journal devoted exclusively to AHP. The International Symposium on the Analytic Hierarchy Process (ISAHP) holds biennial meetings of academics and practitioners interested in the field. A wide range of topics are covered. Those in 2005 ranged from Establishing Payment Standards for Surgical Specialists, to Strategic Technology Roadmapping, to Infrastructure Reconstruction in Devastated Countries. At the 2007 meeting in Valparaiso, Chile, over 90 papers were presented from 19 countries, including the U.S., Germany, Japan, Chile, Malaysia, and Nepal. A similar number of papers were presented at the 2009 symposium in Pittsburgh, Pennsylvania, when 28 countries were represented. Subjects of the papers included Economic Stabilization in Latvia, Portfolio Selection in the Banking Sector, Wildfire Management to Help Mitigate Global Warming, and Rural Microprojects in Nepal. Using the Analytic Hierarchy Process As can be seen in the material that follows, using the AHP involves the mathematical synthesis of numerous judgments about the decision problem at hand. It is not uncommon for these judgments to number in the dozens or even the hundreds. While the math can be done by hand or with a calculator, it is far more common to use one of several computerized methods for entering and synthesizing the judgments. The simplest of these involve standard spreadsheet software, while the most complex use custom software, often augmented by special devices for acquiring the judgments of decision makers gathered in a meeting room. The procedure for using the AHP can be summarized as: These steps are more fully described below. Model the problem as a hierarchy The first step in the Analytic Hierarchy Process is to model the problem as a hierarchy. In doing this, participants explore the aspects of the problem at levels from general to detailed, then express it in the multileveled way that the AHP requires. As they work to build the hierarchy, they increase their understanding of the problem, of its context, and of each other’s thoughts and feelings about both. Hierarchies defined A hierarchy is a stratified system of ranking and organizing people, things, ideas, etc., where each element of the system, except for the top one, is subordinate to one or more other elements. Though the concept of hierarchy is easily grasped intuitively, it can also be described mathematically. Diagrams of hierarchies are often shaped roughly like pyramids, but other than having a single element at the top, there is nothing necessarily pyramid-shaped about a hierarchy. Human organizations are often structured as hierarchies, where the hierarchical system is used for assigning responsibilities, exercising leadership, and facilitating communication. Familiar hierarchies of “things” include a desktop computer’s tower unit at the “top,” with its subordinate monitor, keyboard, and mouse “below.” In the world of ideas, we use hierarchies to help us acquire detailed knowledge of complex reality: we structure the reality into its constituent parts, and these in turn into their own constituent parts, proceeding down the hierarchy as many levels as we care to. At each step, we focus on understanding a single component of the whole, temporarily disregarding the other components at this and all other levels. As we go through this process, we increase our global understanding of whatever complex reality we are studying. Think of the hierarchy that medical students use while learning anatomy—they separately consider the musculoskeletal system (including parts and subparts like the hand and its constituent muscles and bones), the circulatory system (and its many levels and branches), the nervous system (and its numerous components and subsystems), etc., until they’ve covered all the systems and the important subdivisions of each. Advanced students continue the subdivision all the way to the level of the cell or molecule. In the end, the students understand the “big picture” and a considerable number of its details. Not only that, but they understand the relation of the individual parts to the whole. By working hierarchically, they’ve gained a comprehensive understanding of anatomy. Similarly, when we approach a complex decision problem, we can use a hierarchy to integrate large amounts of information into our understanding of the situation. As we build this information structure, we form a better and better picture of the problem as a whole. Hierarchies in the AHP An AHP hierarchy is a structured means of modeling the decision at hand. It consists of an overall goal, a group of options or alternatives for reaching the goal, and a group of factors or criteria that relate the alternatives to the goal. The criteria can be further broken down into subcriteria, sub-subcriteria, and so on, in as many levels as the problem requires. A criterion may not apply uniformly, but may have graded differences like a little sweetness is enjoyable but too much sweetness can be harmful. In that case the criterion is divided into subcriteria indicating different intensities of the criterion, like: little, medium, high and these intensities are prioritized through comparisons under the parent criterion, sweetness. Published descriptions of AHP applications often include diagrams and descriptions of their hierarchies; some simple ones are shown throughout this article. More complex AHP hierarchies have been collected and reprinted in at least one book. More complex hierarchies can be found in this article’s talk page. The design of any AHP hierarchy will depend not only on the nature of the problem at hand, but also on the knowledge, judgments, values, opinions, needs, wants, etc. of the participants in the decision making process. Constructing a hierarchy typically involves significant discussion, research, and discovery by those involved. Even after its initial construction, it can be changed to accommodate newly-thought-of criteria or criteria not originally considered to be important; alternatives can also be added, deleted, or changed. To better understand AHP hierarchies, consider a decision problem with a goal to be reached, three alternative ways of reaching the goal, and four criteria against which the alternatives need to be measured. Such a hierarchy can be visualized as a diagram like the one immediately below, with the goal at the top, the three alternatives at the bottom, and the four criteria in between. There are useful terms for describing the parts of such diagrams: Each box is called a node. A node that is connected to one or more nodes in a level below it is called a parent node. The nodes to which it is so connected are called its children. Applying these definitions to the diagram below, the Goal is the parent of the four Criteria, and the four Criteria are children of the Goal. Each Criterion is a parent of the three Alternatives. Note that there are only three Alternatives, but in the diagram, each of them is repeated under each of its parents. To reduce the size of the drawing required, it is common to represent AHP hierarchies as shown in the diagram below, with only one node for each alternative, and with multiple lines connecting the alternatives and the criteria that apply to them. To avoid clutter, these lines are sometimes omitted or reduced in number. Regardless of any such simplifications in the diagram, in the actual hierarchy each alternative is connected to every one of its parent nodes. Evaluate the hierarchy Once the hierarchy has been constructed, the participants analyze it through a series of pairwise comparisons that derive numerical scales of measurement for the nodes. The criteria are pairwise compared against the goal for importance. The alternatives are pairwise compared against each of the criteria for preference. The comparisons are processed mathematically, and priorities are derived for each node. Consider the “Choose a Leader” example above. An important task of the decision makers is to determine the weight to be given each criterion in making the choice of a leader. Another important task is to determine the weight to be given to each candidate with regard to each of the criteria. The AHP not only lets them do that, but it lets them put a meaningful and objective numerical value on each of the four criteria. Establish priorities This section explains priorities, shows how they are established, and provides a simple example. Priorities defined and explained Priorities are numbers associated with the nodes of an AHP hierarchy. They represent the relative weights of the nodes in any group. Like probabilities, priorities are absolute numbers between zero and one, without units or dimensions. A node with priority .200 has twice the weight in reaching the goal as one with priority .100, ten times the weight of one with priority .020, and so forth. Depending on the problem at hand, “weight” can refer to importance, or preference, or likelihood, or whatever factor is being considered by the decision makers. Priorities are distributed over a hierarchy according to its architecture, and their values depend on the information entered by users of the process. Priorities of the Goal, the Criteria, and the Alternatives are intimately related, but need to be considered separately. By definition, the priority of the Goal is 1.000. The priorities of the Alternatives always add up to 1.000. Things can become complicated with multiple levels of Criteria, but if there is only one level, their priorities also add to 1.000. All this is illustrated by the priorities in the example below. Observe that the priorities on each level of the example—the Goal, the Criteria, and the Alternatives—all add up to 1.000. The priorities shown are those that exist before any information has been entered about weights of the criteria or alternatives, so the priorities within each level are all equal. They are called the hierarchy’s default priorities. If a fifth Criterion were added to this hierarchy, the default priority for each Criterion would be .200. If there were only two Alternatives, each would have a default priority of .500. Two additional concepts apply when a hierarchy has more than one level of criteria: local priorities and global priorities. Consider the hierarchy shown below, which has several Subcriteria under each Criterion. The local priorities, shown in gray, represent the relative weights of the nodes within a group of siblings with respect to their parent. You can easily see that the local priorities of each group of Criteria and their sibling Subcriteria add up to 1.000. The global priorities, shown in black, are obtained by multiplying the local priorities of the siblings by their parent’s global priority. The global priorities for all the subcriteria in the level add up to 1.000. The rule is this: Within a hierarchy, the global priorities of child nodes always add up to the global priority of their parent. Within a group of children, the local priorities add up to 1.000. So far, we have looked only at default priorities. As the Analytical Hierarchy Process moves forward, the priorities will change from their default values as the decision makers input information about the importance of the various nodes. They do this by making a series of pairwise comparisons. Practical examples Experienced practitioners know that the best way to understand the AHP is to work through cases and examples. Two detailed case studies, specifically designed as in-depth teaching examples, are provided as appendices to this article: Some of the books on AHP contain practical examples of its use, though they are not typically intended to be step-by-step learning aids. One of them contains a handful of expanded examples, plus about 400 AHP hierarchies briefly described and illustrated with figures. Many examples are discussed, mostly for professional audiences, in papers published by the International Symposium on the Analytic Hierarchy Process. Criticisms The AHP is included in most operations research and management science textbooks, and is taught in numerous universities; it is used extensively in organizations that have carefully investigated its theoretical underpinnings. While the general consensus is that it is both technically valid and practically useful, the method does have its critics. Most of the criticisms involve a phenomenon called rank reversal, discussed in the following section. Rank reversal Decision making involves ranking alternatives in terms of criteria or attributes of those alternatives. It is an axiom of some decision theories that when new alternatives are added to a decision problem, the ranking of the old alternatives must not change — that “rank reversal” must not occur. The reasonableness of this axiom for all applications is questionable, since there are real-world examples where adding new alternatives can change the rank of the old ones. There are also situations where it is not reasonable for the rank of existing alternatives to change when a new alternative that is not as good as any of the existing alternatives is added for consideration. The 2000 U.S. presidential election is an example of a decision that can be understood as involving rank reversal. Ralph Nader was an ‘irrelevant’ alternative, in that he was dominated by both the Democrat and Republican candidates. However, since he may have attracted more votes from those who would have voted Democratic rather than Republican, his presence caused the ranks to reverse. Put another way, if Nader were not in the race, it is conceivable that Al Gore would have won. The same could be said for the impact that Ross Perot had on George Bush’s loss in 1992. There are two schools of thought about rank reversal. One maintains that new alternatives that introduce no additional attributes should not cause rank reversal under any circumstances. The other maintains that there are some situations in which rank reversal can reasonably be expected. The original formulation of AHP allowed rank reversals. In 1993, Forman introduced a second AHP synthesis mode, called the ideal synthesis mode, to address choice situations in which the addition or removal of an ‘irrelevant’ alternative should not and will not cause a change in the ranks of existing alternatives. The current version of the AHP can accommodate both these schools — its Ideal Mode preserves rank, while its Distributive Mode allows the ranks to change. Either mode is selected according to the problem at hand. Rank reversal and the AHP are extensively discussed in a 2001 paper in Operations Research, as well as a chapter entitled Rank Preservation and Reversal, in the current basic book on AHP. The latter presents published examples of rank reversal due to adding copies and near copies of an alternative, due to intransitivity of decision rules, due to adding phantom and decoy alternatives, and due to the switching phenomenon in utility functions. It also discusses the Distributive and Ideal Modes of the AHP.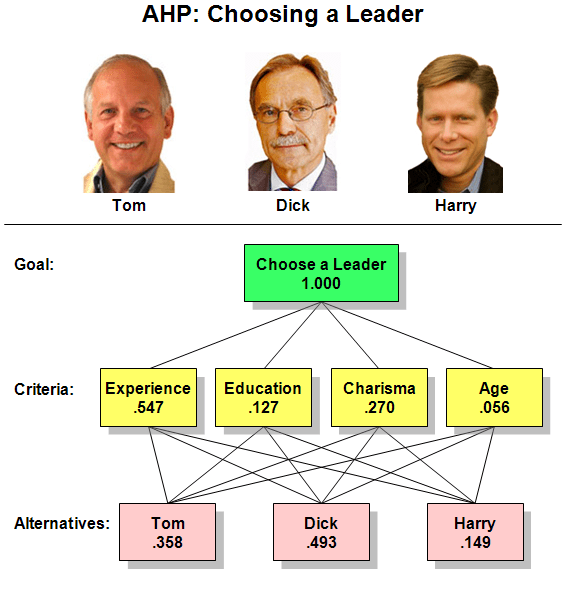

A typical device for entering judgments in an AHP group decision making session
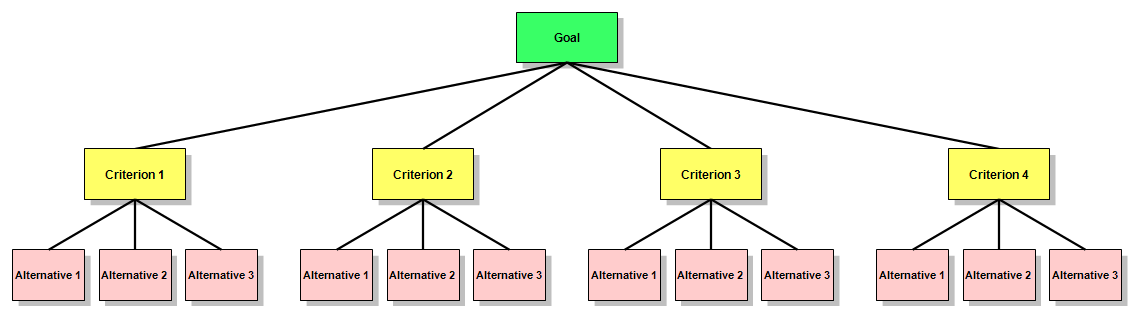
A simple AHP hierarchy. There are three Alternatives for reaching the Goal, and four Criteria to be used in deciding among them.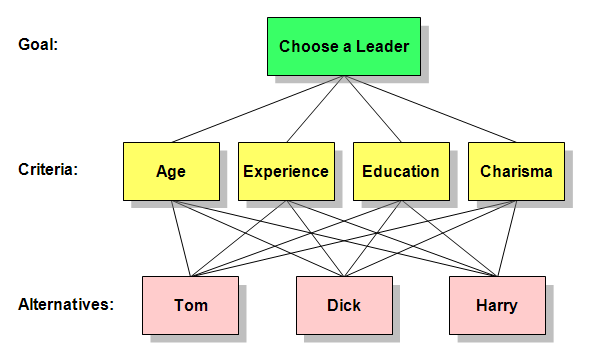
AHP hierarchy for choosing a leader. There is one goal, three candidates and four criteria for choosing among them.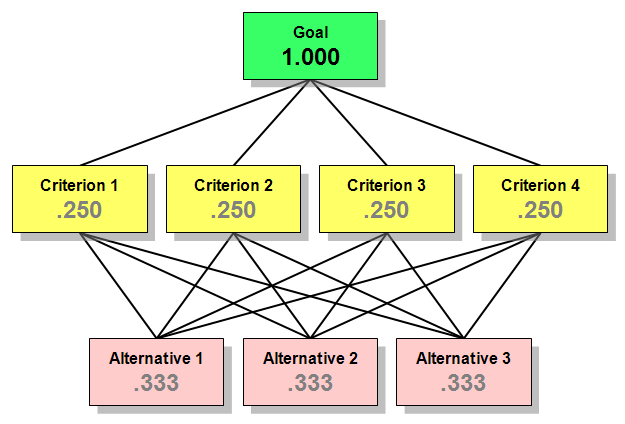
Simple AHP hierarchy with associated default priorities.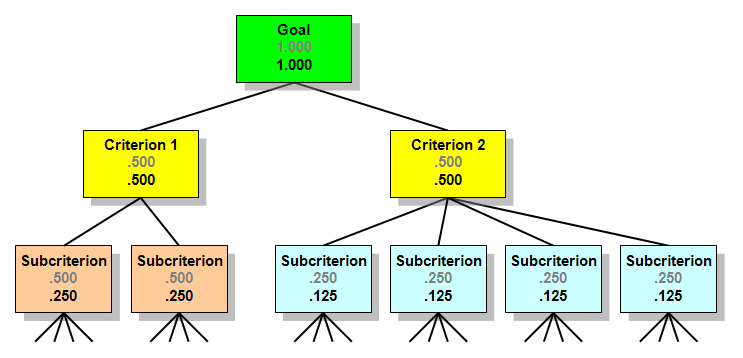
A more complex AHP hierarchy, with local and global default priorities. In the interest of clarity, the decision alternatives do not appear in the diagram.