Abstraction is a concept that has intrigued and perplexed scholars and thinkers for centuries. It is the process of simplifying complex ideas and concepts to their essential elements, allowing for a deeper understanding and appreciation of their underlying beauty. From mathematics to art, abstraction has played a crucial role in shaping our understanding of the world around us. In this introduction, we will delve into the multifaceted nature of abstraction and how it has been used to unravel the complexities of our existence, revealing the true essence and beauty of the world.
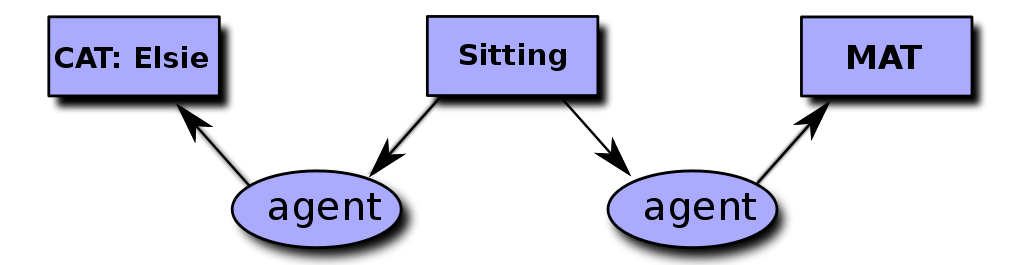
Abstraction is a process by which higher concepts are derived from the usage and classification of literal (“real” or “concrete”) concepts, first principles, or other methods. An “abstraction” (noun) is a concept that acts as super-categorical noun for all subordinate concepts, and connects any related concepts as a group, field, or category. Abstractions may be formed by reducing the information content of a concept or an observable phenomenon, typically to retain only information which is relevant for a particular purpose. For example, abstracting a leather soccer ball to the more general idea of a ball retains only the information on general ball attributes and behavior, eliminating the characteristics of that particular ball. Origins The first symbols of abstract thinking in humans can be traced to fossils dating between 50,000 and 100,000 years ago in Africa. However, language itself, whether spoken or written, involves abstract thinking. Thought process In philosophical terminology, abstraction is the thought process wherein ideas are distanced from objects. Abstraction uses a strategy of simplification, wherein formerly concrete details are left ambiguous, vague, or undefined; thus effective communication about things in the abstract requires an intuitive or common experience between the communicator and the communication recipient. This is true for all verbal/abstract communication. Cat on Mat (picture 1) For example, many different things can be red. Likewise, many things sit on surfaces (as in picture 1, to the right). The property of redness and the relation sitting-on are therefore abstractions of those objects. Specifically, the conceptual diagram graph 1 identifies only three boxes, two ellipses, and four arrows (and their five labels), whereas the picture 1 shows much more pictorial detail, with the scores of implied relationships as implicit in the picture rather than with the nine explicit details in the graph. Graph 1 details some explicit relationships between the objects of the diagram. For example the arrow between the agent and CAT:Elsie depicts an example of an is-a relationship, as does the arrow between the location and the MAT. The arrows between the gerund SITTING and the nouns agent and location express the diagram’s basic relationship; “agent is SITTING on location”; Elsie is an instance of CAT. Conceptual graph for A Cat sitting on the Mat (graph 1) Although the description sitting-on (graph 1) is more abstract than the graphic image of a cat sitting on a mat (picture 1), the delineation of abstract things from concrete things is somewhat ambiguous; this ambiguity or vagueness is characteristic of abstraction. Thus something as simple as a newspaper might be specified to six levels, as in Douglas Hofstadter’s illustration of that ambiguity, with a progression from abstract to concrete in Gödel, Escher, Bach (1979): An abstraction can thus encapsulate each of these levels of detail with no loss of generality. But perhaps a detective or philosopher/scientist/engineer might seek to learn about some thing, at progressively deeper levels of detail, to solve a crime or a puzzle. Referents Abstractions sometimes have ambiguous referents; for example, “happiness” (when used as an abstraction) can refer to as many things as there are people and events or states of being which make them happy. Likewise, “architecture” refers not only to the design of safe, functional buildings, but also to elements of creation and innovation which aim at elegant solutions to construction problems, to the use of space, and to the attempt to evoke an emotional response in the builders, owners, viewers and users of the building. Instantiation Things that do not exist at any particular place and time are often considered abstract. By contrast, instances, or members, of such an abstract thing might exist in many different places and times. Those abstract things are then said to be multiply instantiated, in the sense of picture 1, picture 2, etc., shown above. It is not sufficient, however, to define abstract ideas as those that can be instantiated and to define abstraction as the movement in the opposite direction to instantiation. Doing so would make the concepts “cat” and “telephone” abstract ideas since despite their varying appearances, a particular cat or a particular telephone is an instance of the concept “cat” or the concept “telephone”. Although the concepts “cat” and “telephone” are abstractions, they are not abstract in the sense of the objects in graph 1 above. We might look at other graphs, in a progression from cat to mammal to animal, and see that animal is more abstract than mammal; but on the other hand mammal is a harder idea to express, certainly in relation to marsupial or monotreme. Physicality A physical object (a possible referent of a concept or word) is considered concrete (not abstract) if it is a particular individual that occupies a particular place and time. Abstract things are sometimes defined as those things that do not exist in reality or exist only as sensory experiences, like the color red. That definition, however, suffers from the difficulty of deciding which things are real (i.e. which things exist in reality). For example, it is difficult to agree to whether concepts like God, the number three, and goodness are real, abstract, or both. An approach to resolving such difficulty is to use predicates as a general term for whether things are variously real, abstract, concrete, or of a particular property (e.g. good). Questions about the properties of things are then propositions about predicates, which propositions remain to be evaluated by the investigator. In the graph 1 above, the graphical relationships like the arrows joining boxes and ellipses might denote predicates. Different levels of abstraction might be denoted by a progression of arrows joining boxes or ellipses in multiple rows, where the arrows point from one row to another, in a series of other graphs, say graph 2, etc. Abstraction used in philosophy Abstraction in philosophy is the process (or, to some, the alleged process) in concept-formation of recognizing some set of common features in individuals, and on that basis forming a concept of that feature. The notion of abstraction is important to understanding some philosophical controversies surrounding empiricism and the problem of universals. It has also recently become popular in formal logic under predicate abstraction. Another philosophical tool for discussion of abstraction is thought space. In the Urantia Book glossary Dr. William S. Sadler commented that “Philosophers commit their gravest error when they are misled into the fallacy of abstraction, the practice of focusing the attention upon one aspect of reality and then of pronouncing such an isolated aspect to be the whole truth.” (42.6) 2:7.5 Ontological status The way that physical objects, like rocks and trees, have being differs from the way that properties of abstract concepts or relations have being, for example the way the concrete, particular, individuals pictured in picture 1 exist differs from the way the concepts illustrated in graph 1 exist. That difference accounts for the ontological usefulness of the word “abstract”. The word applies to properties and relations to mark the fact that, if they exist, they do not exist in space or time, but that instances of them can exist, potentially in many different places and times. Perhaps confusingly, some philosophies refer to tropes (instances of properties) as abstract particulars. E.g., the particular redness of a particular apple is an abstract particular. Akin to qualia and sumbebekos. In linguistics Reification, also called hypostatization, might be considered a formal fallacy whenever an abstract concept, such as “society” or “technology” is treated as if it were a concrete object. In linguistics this is called metonymy, in which abstract concepts are referred to using the same sorts of nouns that signify concrete objects. Metonymy is an aspect of the English language and of other languages. It can blur the distinction between abstract and concrete things: 1805: Horatio Nelson (Battle of Trafalgar) – “England expects that every man will do his duty” Compression An abstraction can be seen as a process of mapping multiple different pieces of constituent data to a single piece of abstract data based on similarities in the constituent data, for example many different physical cats map to the abstraction “CAT”. This conceptual scheme emphasizes the inherent equality of both constituent and abstract data, thus avoiding problems arising from the distinction between “abstract” and “concrete”. In this sense the process of abstraction entails the identification of similarities between objects and the process of associating these objects with an abstraction (which is itself an object). For example, picture 1 above illustrates the concrete relationship “Cat sits on Mat”. Chains of abstractions can therefore be constructed moving from neural impulses arising from sensory perception to basic abstractions such as color or shape to experiential abstractions such as a specific cat to semantic abstractions such as the “idea” of a CAT to classes of objects such as “mammals” and even categories such as “object” as opposed to “action”. For example, graph 1 above expresses the abstraction “agent sits on location”. This conceptual scheme entails no specific hierarchical taxonomy (such as the one mentioned involving cats and mammals), only a progressive exclusion of detail. The neurology of abstraction A recent meta-analysis suggests that the verbal system has greater engagement for abstract concepts when the perceptual system is more engaged for processing of concrete concepts. This is because abstract concepts elicit greater brain activity in the inferior frontal gyrus and middle temporal gyrus compared to concrete concepts when concrete concepts elicit greater activity in the posterior cingulate, precuneus, fusiform gyrus, and parahippocampal gyrus. Other research into the human brain suggests that the left and right hemispheres differ in their handling of abstraction. For example, one meta-analysis reviewing human brain lesions has shown a left hemisphere bias during tool usage. Abstraction in art Typically, abstraction is used in the arts as a synonym for abstract art in general. Strictly speaking, it refers to art unconcerned with the literal depiction of things from the visible world—it can, however, refer to an object or image which has been distilled from the real world, or indeed, another work of art. Artwork that reshapes the natural world for expressive purposes is called abstract; that which derives from, but does not imitate a recognizable subject is called nonobjective abstraction. In the 20th century the trend toward abstraction coincided with advances in science, technology, and changes in urban life, eventually reflecting an interest in psychoanalytic theory. Later still, abstraction was manifest in more purely formal terms, such as color, freed from objective context, and a reduction of form to basic geometric designs. In music, the term abstraction can be used to describe improvisatory approaches to interpretation, and may sometimes indicate abandonment of tonality. Atonal music has no key signature, and is characterized the exploration of internal numeric relationships. Abstraction in psychology Carl Jung’s definition of abstraction broadened its scope beyond the thinking process to include exactly four mutually exclusive, opposing complementary psychological functions: sensation, intuition, feeling, and thinking. Together they form a structural totality of the differentiating abstraction process. Abstraction operates in one of these opposing functions when it excludes the simultaneous influence of the other functions and other irrelevancies, such as emotion. Abstraction requires selective use of this structural split of abilities in the psyche. The opposite of abstraction is concretism. Abstraction is one of Jung’s 57 definitions in Chapter XI of Psychological Types. There is an abstract thinking, just as there is abstract feeling, sensation and intuition. Abstract thinking singles out the rational, logical qualities … Abstract feeling does the same with … its feeling-values. … I put abstract feelings on the same level as abstract thoughts. … Abstract sensation would be aesthetic as opposed to sensuous sensation and abstract intuition would be symbolic as opposed to fantastic intuition. (Jung, [1921] (1971):par. 678). Abstraction in computer science Computer scientists use abstraction and communicate their solutions with the computer in some particular computer language. Abstraction allows program designers to separate categories and concepts from instances of implementation, so that they do not depend on software or hardware. Abstraction in mathematics Abstraction in mathematics is the process of extracting the underlying essence of a mathematical concept, removing any dependence on real world objects with which it might originally have been connected, and generalizing it so that it has wider applications or matching among other abstract descriptions of equivalent phenomena. The advantages of abstraction in mathematics are: The main disadvantage of abstraction is that highly abstract concepts are more difficult to learn, and require a degree of mathematical maturity and experience before they can be assimilated.