Experimental design provides the logical architecture for scientific research examining causal relationships. Most people intuitively recognize causal relationships. It is not uncommon to hear, for instance, that increased time studying caused an improved test grade, that a “sweet tooth” enabled a friend’s weight gain, or that traffic congestion instigated a “road rage” incident. The tendency to attribute causality, often spontaneously, in commonsense explanations of everyday behaviors punctuates both private and public discourse and appears a distinctively human characteristic (Frey et al. 2000).
In scientific endeavors, we are typically much more deliberate when making causality inferences (Hill 1965) and often rely on experimentation to inform judgments about causal relationships. Experimentation is a process used to determine the extent, if any, of causal connections between two or more variables. Through experimentation, we test predictions about causal relationships by manipulating aspects of a particular context or activity and then observing the resulting perceptual and behavioral outcomes.
Basic Characteristics Of Experimental Design
Effective experimentation is guided by a testable descriptive causal hypothesis asserting the conditions under which a manipulable independent variable, commonly called an “experimental treatment” or “intervention,” involving at least two levels, influences measurable outcomes or dependent variables. Experimentation typically incorporates systematic procedures maximizing, to the extent possible, the researcher’s ability to guard against or control circumstances that might provide alternative or rival explanations threatening the validity of causal explanations. Unfortunately, when working with human research participants, an inverse relationship often emerges between the extent of control exercised in experimentation and the generalizability of subsequent research findings. Equally important, sometimes, even when experimentation is possible, ethical considerations preclude its use.
Experimental design is the logical system providing the foundational framework for experimentation utilizing well-developed principles of scientific inquiry. Contemporary understanding of experimental design has emerged from the incremental accumulation of new concepts and practices proposed by a range of scholars working in diverse disciplines (e.g., agriculture, education, health/medicine, psychology, and statistics) over the last hundred years (Cochran & Cox 1957; Fisher 1971; Kirk 1995; Winer 1971).
Two concepts, randomization and control, are the cornerstones of experimental design. Randomization, first popularized by McCall (1923) and Fisher (1925), refers to the assignment of research participants to treatment groups or conditions (i.e., levels of an independent variable) based on mere chance. Random assignment can be accomplished using any procedure (e.g., tossing a fair coin) in which each participant has a nonzero probability of being assigned to each treatment group. For instance, in an experiment with two conditions (control vs treatment), on a “coin toss” yielding heads, a research participant would be assigned to the control condition; but if tails comes up, the research participant goes into the treatment condition.
Control, in experimental design, involves holding constant or systematically varying extraneous variables (e.g., mediators, confounders, and suppressors) to minimize their effect on the focal causal relationship. Campbell and Stanley (1963; also see Shadish et al. 2002) were instrumental in articulating the critical importance of control in experimental design. In their seminal work, Experimental and quasi-experimental designs for research, they identified 12 factors jeopardizing the internal and external validity of various experimental design configurations. They outlined eight different classes of extraneous variables that, “if not controlled in the experimental design” (p. 5), might threaten the study’s internal validity and obscure otherwise meaningful findings. These factors – including history, maturation, testing, instrumentation, statistical regression, selection bias, and experimental mortality – are detailed elsewhere on this website. Factors jeopardizing external validity or generalizability included reactive or interactive effects resulting from participant selection, experimental arrangements, and outcome assessment.
Types Of Experimental Designs
Incorporating these threats to research validity, Campbell and Stanley also advanced a comprehensive typology of experimental design configurations. Specifically, they divided designs for experimental into four general types: (1) pre-experimental designs, (2) true experimental designs, (3) quasi-experimental designs, and (4) ex post facto designs. To facilitate description of experimental designs a standardized notation has been developed.
When research participants are exposed to an experimental treatment (i.e., independent variable) the letter X is used. The letter O indicates an outcome or dependent variable measurement. The absence of a manipulative treatment (X) is indicated by the symbol “__” and the letter R denotes random assignment to experimental treatments. Directionality, which refers to the temporal order in which a treatment (X) and outcome (O) occur, is symbolized as “→” when forward and “←” when backward. Treatments (X) and outcomes (O) presented vertically take place simultaneously.
Pre-Experimental Designs
Three configurations are categorized as pre-experimental designs including the “one-shot case study” (X→O), the “one-group pre-test/post-test design” (O1→X→O2), and the “static-group comparison” (Fig. 1). Although these configurations have been frequently employed in endeavors testing causal relationships, they lack many of the basic characteristics crucial for effective experimentation (e.g., random assignment, control of validity threats, equitably treated comparison groups) and afford little or no utility for testing causal inferences. The horizontal line separating the treatment groups in Figure 1, for instance, highlights the absence of random assignment in the static-group comparison pre-experimental design.
Figure 1 Static-group comparison pre-experimental design
True Experimental Designs
Randomization and the inclusion of controls against threats to internal validity are fundamental to the three configurations within the true experimental designs category. For instance, the pre-test/post-test control group design (Fig. 2), considered by many to be the “old work-horse” of traditional experimentation, controls for eight threats to internal validity if effectively implemented. Randomly assigned from the same sample to both the treatment (X) and control (___) groups, research participants are first observed prior to treatment via a pre-test (O1). The first group then receives the experimental treatment (X) while the second group, called the control group, engages a comparable, but unrelated, task (___) and both groups complete a post-test assessment. The differences between the pre-test and the post-test (O2 – O1) are compared between the treatment and control group. If this comparison yields a significant difference then we assume that the experimental treatment was the primary cause. The randomized controlled trial, a mainstay in health communication and health-related disciplines, is a refinement of the basic pre-test/ post-test control group design that incorporates several contemporary methodological guidelines intended to enhance both validity and generalizability.

Figure 2 Pre-test/post-test control group design
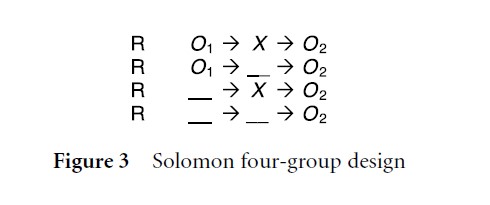
Figure 3 Solomon four-group design
The Solomon four-group design (Fig. 3) is an extension of the previous configuration and perhaps is the most precise and powerful experimental approach. In order to minimize any potential negative consequences resulting from testing, the design incorporates each pre-test and treatment alternative. Systematic comparisons across the six pre and posttest assessments allow the researcher to check both the efficacy of randomization and for any interaction between the pre-test (O1) and the treatment (X ). Practical considerations, in particular the required additional resources (i.e., research participant, time, and money), appear to have limited the popularity of this experimental design.
Recognizing that the pre-test, while a deeply embedded practice in social/behavioral sciences, is not an essential component of a true experimental design, Campbell and Stanley detailed the post-test-only control group design (Fig. 4). This design is particularly effective in circumstances where a pre-test is ill-advised because it could sensitize research participants or where limited resources require an efficient research implementation. The crucial role of random assignment distinguishes this design from the “static-group comparison” pre-experimental design outlined above.
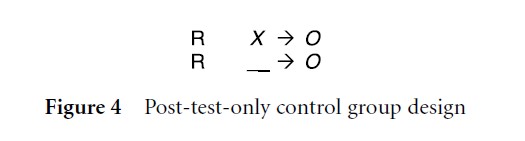
Figure 4 Post-test-only control group design
While these simple, single independent variable or one-factor experimental designs promote conceptual clarity, their application in contemporary research activities is relatively rare. Instead, researchers often elaborate on the conceptual basis of the pre-test/ post-test control group and the post-test-only control group designs to produce factorial designs. A factorial design involves the simultaneous analysis of two (two-factor design), three (three-factor design), or more independent variables within the same experimental design. Factorial designs, unlike the one-factor designs detailed above, permit examination of the interaction or interdependence between two or more factors or independent variables in the effects they produce on the outcome or dependent variable.
The repeated-measures design is another variant commonly employed in social and behavioral science research. The previously detailed experimental designs all involve a between-group structure in that research participants are assigned to a particular treatment group (a level of the manipulated independent variable), their outcome measures are combined as group outcomes, and then differences between group outcomes are analyzed. The between-group structure, for example, guides the analytical process outlined for the pre-test/post-test control group design above. The repeated-measures design, on the other hand, involves multiple assessments of a single outcome or set of outcomes within each research participant. In repeated-measures designs, research participants encounter and respond to every level of an experimental treatment so that the effects of such manipulations materialize as variations within each individual’s pattern of outcomes rather than as differences between groups of people.
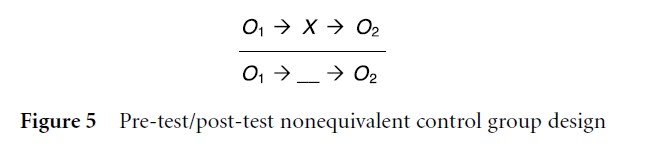
Figure 5 Pre-test/post-test nonequivalent control group design
Quasi-Experimental Designs
Research situations can arise in which the random selection and assignment of research participants is not possible. Experimentation undertaken under such conditions can utilize quasi-experimental designs. These nonrandomized designs, while providing valuable information, must be recognized as involving basic faults that can influence data interpretation. The strongest and most widely used quasi-experimental design is the pre-test/ post-test nonequivalent control group design (Fig. 5). This design differs from the true experimental designs because the test and control group are not randomly assigned (emphasized by the horizontal line) and, consequently, are not equivalent. Deliberate comparison of the pre-test results reveals the degree of equivalency between the treatment (X) and control (___) groups.
Other quasi-experimental designs advanced by Campbell and Stanley are all built on the notion of serialized assessment of the dependent measure both before and after the introduction of an experimental treatment (O1 O2→X→O3 O4). If substantial change follows introduction of the treatment then there is reason to suspect that the treatment caused the observed change. Referred to as “time series designs,” these configurations can be expanded to incorporate multiple treatment levels (i.e., a control group in the simplest form) and other variants intended to bolster validity.
Ex Post Facto Designs
Often characterized as “experimentation in reverse,” the ex post facto design has emerged as an important investigative tool for researchers in behavioral and social sciences. Commonly referred to as a case-control study (Fig. 6; Gordis 2004), the general concept underlying this design is to identify individuals with an outcome or consequence of interest (case group) and, following backward directionality, compare their experiences (i.e., antecedent variables) to a similar group without the outcome of interest (control group). Research participant matching is used in the strongest form of this design to minimize potential threats to validity. The case-control study design, it must be recognized, employs observational data. Consequently, interpretation of findings requires careful consideration of several criteria, such as biological, environmental, and temporal plausibility, before causation can be projected (Hill 1965).

Figure 6 Case-control study
Emerging Trends
The simple designs for experimentation summarized here continue to provide the essential logical building blocks for much contemporary research. At the same time, however, it is important to recognize that these designs are, at least to some extent, bounded by the era in which they were articulated. We often forget that the work of most researchers was aided by slide-rules and mechanical calculators when these designs were proposed. Contemporary advances in both computer technologies and statistical software have, of course, substantially expanded our analytical prowess and, as a result, the sophistication of experimental designs.
Factorial designs involving several independent variables, mixed-measures models combining factorial and repeated-measures designs, and multivariate designs that simultaneously include multiple dependent measures – all of which were emerging trends just three decades ago – are now commonplace (Smith et al. 2002). And new developments, such as multilevel modeling (Luke 2004), which promotes experimentation in diverse cultural, social, and behavioral contexts, are rapidly evolving. Nevertheless, the basic tenets of experimental design outlined here remain as the benchmarks for scientific inquiry, attempting to satisfy our distinctively human desire to understand causality and causal relationship.
References:
- Campbell, D. T., & Stanley, J. C. (1963). Experimental and quasi-experimental designs for research. Boston: Houghton Mifflin.
- Cochran, W. G., & Cox, G. M. (1957). Experimental designs, 2nd edn. New York: Wiley.
- Fisher, R. A. (1925). Statistical methods for research workers. London: Oliver and Boyd.
- Fisher, R. A. (1971). The design of experiments. London: Oliver and Boyd. (Original work published 1935).
- Frey, L., Botan, K., & Kreps, G. (2000). Investigating communication. New York: Allyn and Bacon.
- Gordis, L. (2004). Epidemiology, 3rd edn. Philadephia, PA: Elsevier Saunders.
- Hill, A. B. (1965). The environment and disease: Association or causation? Proceedings of the Royal Society of Medicine, 58, 295 –300.
- Kirk, R. E. (1995). Experimental design: Procedures for the behavioral sciences, 3rd edn. Pacific Grove, CA: Brooks/Cole.
- Luke, D. A. (2004). Multilevel modeling. Thousand Oaks, CA: Sage.
- McCall, W. A. (1923). How to experiment in education. New York: Macmillan.
- Moher, D., Schulz, K. F., & Altman, D. for the CONSORT Group (2001). The CONSORT statement: Revised recommendations for improving the quality of reports of parallel-group randomized trials. Journal of the American Medical Association, 285, 1987–1991.
- Shadish, W. R., Cook, T. D., & Campbell, D. T. (2002). Experimental and quasi-experimental designs for generalized causal inference. Boston: Houghton Mifflin.
- Smith, R. A., Levine, T. R., Lachlan, K. A., & Fediuk, T. A. (2002). The high cost of complexity in experimental design and data analysis: Type I and type II error rates in multiway ANOVA. Human Communication Research, 28, 515 –530.
- Winer, B. J. (1971). Statistical principles in experimental design, 2nd edn. New York: McGraw-Hill.